Math Lit A Pathway To College Mathematics Pdf

Abstract

Mathematical literacy (ML) is considered central to the application of mathematical knowledge in everyday life and thus is found in many comparative international educational standards. However, there exists barely any evidence about predictors and outcomes of ML having a lasting effect on achievement in nonmathematical domains. We drew on a large longitudinal sample of N = 4001 secondary school students in Grades 5 to 9 and tested for effects of ML on later academic achievement. We took prior achievement in different domains (information and communication technology literacy, scientific literacy, reading comprehension, and listening comprehension), socioeconomic status, and gender into account and investigated predictive effects of math grade, mathematical self-concept, reasoning, and prior achievement on ML. Using structural equation models, we found support for the importance of integrating multiple predictors and revealed a transfer effect of ML on achievement in different school domains. The findings highlight the importance of ML for school curricula and lasting educational decisions.

Introduction

Learning mathematics is oftentimes assumed to be learning for everyday life. We share this assumption and frame it in educational standards. According to the Program for International Student Assessment (PISA; Organisation for Economic Co-operation and Development (OECD) 2019), Mathematical literacy (ML) is defined as "an individual's capacity to formulate, employ, and interpret mathematics in a variety of contexts." The importance of ML as an element in the definition of educational standards has been made apparent in, for example, the USA and Germany (National Council of Teachers of Mathematics 2003; Standing Conference of the Ministers of Education and Cultural Affairs of the Federal Republic of Germany 2004). ML is crucial for students' understanding of mathematics in today's life contexts (Baumert et al. 2007).

International educational studies such as PISA and the Trends in International Mathematics and Science Study (TIMSS) aim to assess students' ML by having them solve everyday problems with mathematical means (Mullis et al. 2009; OECD 2003). Researchers have investigated the development of ML by using large-scale longitudinal studies, for instance, in Germany, PISA studies (PISA Plus 2012–2013: OECD 2013; PISA-I-Plus: Prenzel 2006), and by conducting national studies, for instance the COACTIV ^{Footnote 1} research program (Kunter et al. 2013), the Study of Initial Achievement Levels and Academic Growth in Secondary Schools in the City of Hamburg (e.g., Caro and Lehmann 2009), and the longitudinal Element study (Lehmann and Nikolova 2007).

This large body of research investigating predictors and outcomes of ML has generated partly contradictory results. Among others, prior achievement, migration, and social background (Kiemer et al. 2017), socioeconomic status (Caro and Lehmann 2009), self-efficacy, self-concept, interest, and learning goals (Kriegbaum et al. 2015) were identified as relevant predictors of ML. For the relationship between ML and achievement in other domains, such as reading, studies using longitudinal data found covariation effects in Grades 1 to 7 (Korpipää et al. 2017) and predictive effects of third-grade reading comprehension on ML throughout early primary school when controlling for prior achievement (Grimm 2008).

Hence, ML is also thought to determine later academic achievement in many ways (cf., Duncan et al. 2007; Gut et al. 2012; Siegler et al. 2012). In the context of solving realistic problems, studies on mathematical word problems, mathematical modeling competence, and mathematical problem-solving in general showed that predictors such as calculation skills, mathematical self-concept, reading comprehension, and cognitive skills are relevant for ML development and the relationship to later achievement (Blum and Borromeo Ferri 2009; Brown and Stillman 2017; Leiss et al. 2010; Leutner et al. 2012; Phonapichat et al. 2014). Studies on mathematical modeling, which is typically considered a cognitive process consisting of different phases of solving a real-world problem by means of mathematics, showed that reading comprehension, cognitive skills, and self-concept are important predictors of problem-solving success (Jensen 2007; Leiss et al. 2010; Maass 2006).

However, as argued in a recent study on teaching practice in ML (Kuger et al. 2017), the influence of single predictors is often overestimated, especially in cross-sectional analyses. Therefore, longitudinal studies that take various predictors comprehensively into account are necessary. Furthermore, the empirical support that does exist for predictors and outcomes of ML is mostly restricted to early primary school (e.g., Grimm 2008; Korpipää et al. 2017) or tertiary education (e.g., Hwang and Riccomini 2016; Pape and Wang 2003; Sokolowski 2015). Only a few studies are related to secondary school (Caro and Lehmann 2009; Kriegbaum et al. 2015). Hence, we argue that longitudinal studies across secondary school are needed to examine the influence of ML on later academic achievement while at the same time taking its crucial predictors into account.

Theoretical background of ML

The relationship between ML, reading, and achievement in other domains

We understand academic achievement as achievement in different school domains, for instance, mathematics, language, and science. Achievement in most studies is either operationalized as grade point average (GPA) or assessed with achievement tests in the respective domain, sometimes by using multiple-domain tests such as the Wide Range Achievement Test (Wilkinson 1993), the California Achievement Test, or the Stanford Achievement Test (e.g., Sirin 2005). In line with studies on the development of problem-solving competence, we argue that fostering ML results in higher achievement in other domains later on (Leutner et al. 2012). Later academic achievement is assumed to be linked with success in mathematical tasks, because a strong relationship has been found with mathematical performance in general (Duncan et al. 2007).

Recent research on the covariation of ML and reading achievement indicated that gains in ML-related skills such as problem-solving and reasoning as well as cognitive abilities in general lead to better achievement in other domains (Baumert et al. 2012). The authors suggested the cumulative advantage effect (DiPrete and Eirich 2006) as a possible explanation. Additionally, a transfer effect can be assumed; ML involves skills that are shared with other processes, such as reasoning and general cognitive abilities, so gains in ML will support students' progress in other achievement domains. A study comparing adults with PISA students showed that the average ML in adults was on the level of a secondary school student (Ehmke et al. 2005). These authors also showed that ML in adults was linked to an individual's vocational degree. However, research on mathematical modeling mainly focused on distinct phases of the problem-solving process (Baumert et al. 2007; Blomhoj and Jensen 2003; Blum et al. 2004; Jensen 2007; Leiss and Tropper 2014). Intervention studies have shown that teaching students to construct a situational model of a problem given in text or pictorial form improves their ability to solve mathematical problems (English and Watters 2005; Hwang and Riccomini 2016; Kaiser et al. 2015; Schukajlow et al. 2015). This seems to be especially relevant for students with difficulties in learning mathematics (Phonapichat et al. 2014).

With respect to achievement in other domains, a meta-analysis on applying mathematical modeling to support students' mathematical knowledge acquisition at the high school and college level found positive effects of mathematical-modeling techniques on achievement in different content domains (Sokolowski 2015). Hoffman and Spatariu (2008) examined influences on problem-solving efficiency and found middle to high cross-sectional correlations between GPA and performance on a math achievement test as well as between GPA and problem-solving efficiency. When predictors such as reading competence and self-concept were considered using path analysis, lower coefficients were found (Schommer-Aikins et al. 2005). Jordan et al. (2002) showed longitudinally that over 2 years, growth in reading competence was diminished for children with difficulties in mathematical problem-solving. This, again, accounts for the assumption that ML affects achievement in other domains. Moreover, Korpipää et al. (2017) found that reading and arithmetic in Grades 1 to 7 covaried substantially over time.

In summary, reported covariations of ML and achievement in other domains (Jordan et al. 2002; Korpipää et al. 2017; Sokolowski 2015) as well as a relationship between ML and gains in general cognitive abilities (Baumert et al. 2012) hint at common elements in ML and skills relevant to various school domains. This leads to assuming transfer effects of ML on academic achievement. Current research on the relationship between ML and academic achievement is barely conclusive because important predictors remain unconsidered. The necessity for research that takes an integrative view of ML that considers comprehensive predictors and outcomes using longitudinal data is evident.

The role of predictors of ML

A longitudinal study from Chu et al. (2016) on the development of ML that followed children's gains in reading and mathematics achievement while also assessing preliteracy knowledge, intelligence, executive functions, and parental educational background identified all variables assessed as being predictive for children's ML from preschool to kindergarten. The authors concluded that a combination of domain-general and domain-specific abilities plays an important role in ML development. Using a large sample (N = 6020) of 15-year-old German PISA students, Kriegbaum et al. (2015) showed that besides task-specific self-efficacy, intelligence and prior achievement predicted ML 1 year later.

Current research indicates that multiple predictors play a role in the development of ML. These empirically investigated predictors of ML can also be derived from theories on mathematical modeling that view the cognitive process of solving realistic problems as consisting of several distinct but interdependent phases (Leiss and Tropper 2014). Depending on a given task, certain challenges (e.g., reading correctly, extracting the mathematical information, understanding the context) are essential to solving the problem (Kaiser et al. 2015). Predictors of success in mathematical tasks can be deduced from studying these challenges.

As problems are mainly given in text form, reading comprehension was found to be crucial to understanding the problem and its context (Borromeo Ferri 2006). Qualitative studies showed that many students have difficulties comprehending key words (Phonapichat et al. 2014). A middle to high correlation was reported between mathematical reading comprehension and modeling competence (Leiss et al. 2010). Lee et al. (2004) showed that the strength of this relationship is comparable with that of the influence of cognitive skills on solving mathematical word problems. Reading comprehension for a given problem, additionally, seems independent of technical reading skills such as reading speed and accuracy (Vilenius-Tuohimaa et al. 2008).

To correctly solve the mathematics extracted from a problem, basic calculation skills are needed. Leiss et al. (2010) found a positive correlation between students' results in a general mathematics test used as a measure of non-subject-specific mathematics skills and modeling competence. Counting skills were found to be a valid predictor of later problem-solving skills (Aunola et al. 2004). Using multiple regression analysis, Andersson (2007) showed that calculation had an influence on solving word problems that was larger than that of reading comprehension.

Mathematical self-concept is also considered crucial for problem-solving achievement (Pajares and Miller 1994). Additionally, academic self-concept was demonstrated to play a role in achievement in many school domains (e.g., Marsh et al. 2005). Examining reciprocal effects of mathematical self-concept and achievement, Marsh et al. (2005) found significant path coefficients favoring the effect of self-concept on later achievement. This finding seems to be domain specific (Schöber et al. 2018). Self-efficacy was found to be linked with efficient problem-solving (Hoffman and Spatariu 2008). Belief in one's own capability to solve mathematical problems was also found to be linked with problem-solving performance (Schommer-Aikins et al. 2005). Also gender differences seem to play a role in this relationship: Studies found that boys, especially when stereotypes were evident, outperformed girls when they had higher scores on a self-concept measure (Ehrtmann and Wolter 2018; Preckel et al. 2008).

Besides math-related predictors such as basic calculation skills and mathematical self-concept, domain-general abilities, that is, cognitive processes, are found to be associated with ML. Baumert et al. (2007) argued that reasoning skills and mathematical modeling cannot be investigated independently. There exists research on the relationship of subskills of ML and cognitive skills such as working memory and fluid intelligence (Lee et al. 2004; Swanson 2011; Swanson et al. 2008) as well as executive functioning and intelligence (Arán Filippetti and Richaud 2016; Best et al. 2011). Fuchs et al. (2006) conducted path analyses and found significant path coefficients for language comprehension and nonverbal problem-solving skills on solving arithmetic word problems. Taken together, prior calculation skills, mathematical self-concept, reading comprehension, and cognitive skills are theoretically derived as well as empirically studied predictors of ML.

Socioeconomic status and gender

In studies on ML and academic achievement, among several control variables, two in particular seem to play a prominent role: socioeconomic status (SES) and gender (e.g., Grimm 2008). Children of higher SES tend to receive better grades (Lekholm and Cliffordson 2008) and perform better on academic achievement measures (Sirin 2005). Kiemer et al. (2017) found in PISA data that migration status and SES were interconnected because much of the difference in achievement was due to financial resources when prior achievement was controlled for. Over the secondary school years, the achievement gap associated with SES seems to narrow (Caro and Lehmann 2009).

Gender differences have been found in some studies, presumably depending on the operationalization of outcome variables. For instance, Robinson and Lubienski (2011) found that teachers rated female students higher on mathematics and reading, while cognitive assessments suggest males have an advantage in mathematics. We can conclude that it is important to consider gender and SES when investigating the effects of ML on academic achievement.

Objectives of the current study

The current state of research lacks empirical evidence for the relationship between ML and achievement in domains outside mathematical development. However, this is very relevant because educational standards as well as international studies have focused on promoting ML as a means of enabling students to use their mathematical knowledge in their everyday lives (Hwang and Riccomini 2016; Kaiser et al. 2015; Schukajlow et al. 2015). Moreover, studies so far have not paid enough attention to the comprehensive influence of ML on academic achievement in different school domains. Theories on ML indicate that a gain in ML leads to domain-general problem-solving abilities from which students' overall academic achievement could profit in the sense of transfer effects from learning mathematics on other school domains (Baumert et al. 2012; Chu et al. 2016; Korpipää et al. 2017). Assuming common skill sets for reasoning, reading comprehension, and problem-solving, transfer effects from ML to achievement in other school domains are expected.

Several predictors have been empirically documented as having an effect on or being related to ML (Chu et al. 2016; Kriegbaum et al. 2015; Leiss et al. 2010; Marsh et al. 2005). Although calculation skills (Andersson 2007; Aunola et al. 2004), mathematical self-concept (Hoffman and Spatariu 2008; Marsh et al. 2005), reading comprehension (Lee et al. 2004; Leiss et al. 2010), other prior achievement (Kriegbaum et al. 2015), and reasoning (Fuchs et al. 2006) were separately found to be empirically related to ML, research so far has lacked an integrative view of these predictors using longitudinal data to account for effects on both ML and academic achievement in general.

Applying mathematical knowledge in the sense of ML becomes crucial for further mathematical development above the primary-school level, particularly throughout secondary school (United Nations Educational, Scientific and Cultural Organization Institute for Statistics 2013), yet several studies examining mathematical development have focused on primary school (e.g., Duncan et al. 2007; Geary 2011; Korpipää et al. 2017). Furthermore, studies on SES indicate that development in secondary school is a determinant for later achievement because cumulative advantages (Baumert et al. 2012) and the gap between low and high SES (Caro and Lehmann 2009) play an important role at this stage. Thus, it becomes apparent that studies on ML investigating the secondary school years, which constitute an important phase in ML development, are needed.

Hypotheses and research questions

Our study extends previous research by taking an integrative view of ML that considers multiple predictors to explore the effects of ML on later academic achievement, using longitudinal data from a large sample in Grades 5 to 9. Our goal was to investigate how ML predicts academic achievement (information and communication technology (ICT) literacy, scientific literacy, reading comprehension, and listening comprehension) in different school domains throughout secondary school while controlling for prior achievement. We assumed that ML would still have an effect on later academic achievement in different domains when prior achievement in the respective domain is controlled for—in the sense of a transfer effect of ML on achievement in other domains.

We investigated whether existing results regarding predictors of ML can be replicated when a comprehensive set of predictors is studied simultaneously. On the basis of previous findings, we assumed that calculation skills, mathematical self-concept, reasoning, and prior achievement in ML as well as in other domains are linked to later ML. We presumed that these predictors would show effects on ML throughout secondary school when effects of prior achievement are controlled for. Therefore, our research questions and hypotheses are as follows:

1. 1.

   How does ML predict academic achievement in different school domains (i.e., ICT literacy, scientific literacy, reading comprehension, and listening comprehension) throughout the secondary school years?

• Hypothesis 1. ML predicts achievement in different school domains later on even when prior achievement in the respective domain is controlled for.

1. 2.

   How do calculation skills, mathematical self-concept, reading comprehension, and reasoning affect ML when studied comprehensively?

• Hypothesis 2. Calculation skills, mathematical self-concept, reading comprehension, and reasoning predict ML later on when the respective other predictors are controlled for.

As minor questions, we investigated whether hypotheses 1 and 2 are still valid when potential effects of the control variables SES and gender are taken into account.

In sum, it is notable that recent research focused mainly on either preschool and the early school years or high school and college. We examined the postulated relationships from Grades 5 to 9, hence across secondary school.

Method

Sample

We examined our research questions using data from the National Educational Panel Study (NEPS), a longitudinal study conducted in Germany designed for research on educational trajectories (Blossfeld et al. 2011). We used data provided as scientific-use files for registered users of NEPS, which began investigating fifth-grade students in 2010, at two measurement points (Grades 5 or 6, and 9). NEPS provided separate files for competence measures, cohort information, and both student and parent questionnaires, which were prepared for scientific use following professional guidelines and by publishing reports about validity, scaling, and reliability. The original panel cohort consisted of 6112 students, of whom 5778 participated in the first wave in Grade 5. Four years later, 5452 students from the original sample were targeted, of whom 4001 participated in Grade 9 (cf., Zinn et al. 2018). The sample is suited for answering our research questions because this cohort follows students through the course of secondary school (Fabian et al. 2019).

Analyses for testing the postulated hypotheses were conducted with domain-specific competence data (ML, reading, and reasoning) and questionnaire information (math grade, mathematical self-concept, and gender) in Grade 5, domain-specific competence data in Grade 6 (ICT literacy, scientific literacy, and listening comprehension), and the corresponding domain-specific competence data in Grade 9. Information about SES was obtained from parent questionnaires.

The final sample consisted of 4001 students (N = 1963 female (49.4%), missing values in gender: N = 26). Students in Germany in most federal states follow one of three school tracks (Hauptschule, Realschule, or Gymnasium, typically considered general, intermediate, and advanced secondary school, respectively) after the end of Grade 4. In our sample, 51.9% (N = 1701) were allocated to Gymnasium, 30.0% (N = 917) to Realschule, and 7.6% (N = 249) to Hauptschule, thus being fairly representative regarding German school tracks. Relying on the German federal school system, students attending some schools were not yet divided into school tracks (N = 238), and for some students, the declared school track was unclear (N = 722) or missing (N = 174). Regarding SES, 13.8% (N = 418) of students were categorized as having low, 62.9% (N = 1771) intermediate, and 23.3% (N = 668) high SES (missing: N = 1144).

Measures

ML

A mathematical competence assessment was administered consisting of 24 items in Grade 5 and 34 items in Grade 9. The theoretical framework for the mathematics test construction was based on the PISA as well as national educational standards and was designed to measure ML on the basis of mathematical problems from students' life contexts (Neumann et al. 2013). Students were asked to solve mathematical problems and answer mostly multiple-choice questions. As in the PISA, items could be assigned to one of four content areas: quantity, change and relationship, shape and space, and data and chance. Six different cognitive components were distributed over these items with modeling as one of these six components. A sample item titled "The Fence" goes as follows: "Mr. Brown owns a rectangular piece of land that he wants to fence. After calculating, he buys 40 meters of fence. The piece of land has a width of 8 meters. How long is the piece of land?" This item involving modeling belongs to the content area space and shape (Schnittjer and Duchhardt 2015).

Weighted maximum likelihood estimates (WLEs), which are estimates of a student's most likely competence (Pohl and Carstensen 2013), were computed to indicate domain-specific competence. Scaling relies on item response theory (IRT; Pohl and Carstensen 2012). For the following analyses, WLEs of ML were used from Grades 5 to 9, for which sufficient reliabilities (.78 and .81, respectively) have been reported (Duchhardt and Gerdes 2012; Van den Ham et al. 2018). WLEs, theoretically, are standardized scores with M = 0.00 and SD = 1.00, but the values can differ from zero or one, respectively, due to sample selection procedures. Analyses on panel attrition in the NEPS showed that students in this sample with good or medium ML have a stronger tendency to drop out (Zinn et al. 2018). This could mean that students with lower ML are overrepresented in our sample.

Math grade

Students reported their final math grade from the previous year, which, therefore, referred to Grade 4. Students in Grade 4 were not yet divided into school tracks, which enhances the comparability and validity of our measure. Germany uses a grading system of 1 to 6, with 1 indicating the best grade possible. In German-speaking countries, basic calculation skills, for instance, unit operations, are learned in primary school during Grades 1 to 4. For this reason, we argue that math grade at this age represents students' ability in the basic calculation skills needed to solve ML problems, which is why we used it as a measure of mathematical performance in terms of students' calculation skills.

Mathematical self-concept

Mathematical self-concept was conceptualized as domain specific and was geared to the PISA (Wohlkinger et al. 2011). Domain-specific self-concept is widely seen as a subdimension of students' overall academic self-concept and can be investigated in a subject-specific way (Wohlkinger et al. 2016). It was measured using three items (i.e., "I get good grades in mathematics," "Mathematics is one of my best subjects," and "I have always been good at mathematics") with answers ranging from 1 (does not apply at all) to 4 (applies completely) on a 4-point Likert scale. A mean score was calculated from these items. Mathematical self-concept was assessed in Grade 5; Cronbach's alpha for this scale was .87.

ICT literacy

ICT literacy was conceptualized as computer literacy from a functional perspective and relies on everyday problems in modern-day societies (Weinert et al. 2011). Students were presented corresponding problems and asked to accomplish computer-based tasks mostly with screenshots of applications. Moreover, students were asked to answer 30 (Grade 6) or 36 (Grade 9) multiple-choice items. The test was designed to measure students' ability to access, create, manage, and evaluate software applications. ICT literacy was used from Grades 6 to 9, for which sufficient reliabilities (.69 and .81, respectively) were reported (Senkbeil and Ihme 2017; Senkbeil et al. 2014).

Scientific literacy

Scientific literacy was conceptualized as the ability to apply scientific knowledge of personal, social, and global importance in the contexts of environment, technology, and health (Hahn et al. 2013). The test was designed to measure knowledge about matter, systems, development, and interactions in scientific inquiry and reasoning. WLEs were calculated and used from 27 (Grade 6) to 28 (Grade 9) items. Good reliabilities of .77 (Grade 6) and .83 (Grade 9) were reported (Funke et al. 2016; Hahn et al. 2013).

Reading comprehension

Reading comprehension was conceptualized as functional understanding of texts (Gehrer et al. 2013). Students were asked to answer multiple-choice questions about texts meant to represent everyday reading such as information, commentaries, argumentations, instructions, or advertisements. Requirements were categorized into finding information, drawing conclusions, and reflecting texts. Reading comprehension (WLEs) was used from Grades 5 to 9, for which sufficient reliabilities (.77 and .79, respectively) were reported (Pohl et al. 2012; Scharl et al. 2017).

Listening comprehension

Listening comprehension in the NEPS was assessed differently over time. In Grade 6, receptive vocabulary was assessed using an adapted version of the Peabody Picture Vocabulary Test (PPVT; Roßbach et al. 2005). In the PPVT with 77 items in total, students choose one of four pictures based on a given word. Sum scores were calculated for listening comprehension in Grade 6. Cronbach's alpha for this scale was .88.

In Grade 9, listening comprehension was conceptualized as the ability to extract information from spoken texts and to draw conclusions that are implied in these texts (Hecker et al. 2015). In line with the literacy perspective, texts were based on realistic contexts. Students heard two texts (a conversation and a narration) and were asked to answer two sets of eight complex multiple-choice items. Listening comprehension (WLE) was used from Grade 9, for which sufficient reliability (.76) was reported (Rohm et al. 2017).

Reasoning

To measure basic cognitive skills, two tests were constructed for the NEPS: a picture symbol test assessing perceptual speed, and a matrices test assessing reasoning (Haberkorn and Pohl 2013). It has been argued that these two indicators are suitable for assessing fluid intelligence because they are theoretically central and have been empirically found to be crucial for successful development (Brunner et al. 2014). For our study, students' results from the matrices test in Grades 5 and 9 were used to investigate reasoning. Reasoning was assessed using three sets of four items, with Cronbach's alpha = .66 in both grades. Sum scores were calculated, which resulted in a maximum of 12.

SES

In the parent questionnaire at Grade 5, a parent reported his or her highest educational attainment. Responses were rated based on the Comparative Analysis of Social Mobility in Industrial Nations Scale (Brauns et al. 2003). The scale was recoded into three categories: low (no degree or degree with basic work-related training), intermediate (advanced work-related training or postsecondary school), and high (university level or higher), as has been suggested for studies using NEPS data (cf., Zinn et al. 2018).

Modeling issues and missing data

We estimated a structural equation model with regression analyses for assumed paths using the lavaan package in R (R Development Core Team 2008). Fit indices (root mean square error of approximation (RMSEA), confirmatory fit index (CFI), Tucker–Lewis index (TLI)) were used to examine model fit. We applied cutoff values of .06 for RMSEA and .95 for CFI and TLI, which according to Hu and Bentler (1999) indicate a good fit between a hypothesized model and the observed data.

Measurement invariance for ML, ICT literacy, scientific literacy, reading comprehension, and listening comprehension (all by means of WLE) was ensured with an elaborated conceptualization in the NEPS based on models of IRT as well as an anchor-item design (cf., Pohl et al. 2015). It was strengthened by testing for unidimensionality and demonstrating the absence of differential item functioning (e.g., Fischer et al. 2016). Reasoning was measured using the same items on both occasions.

Missing data in single competence tests were already treated when calculating WLEs (cf., Pohl and Carstensen 2013). For missing data in one of the other instruments as well as for participants missing whole competence test assessments, we used a full information maximum likelihood (FIML) approach because statistical power is maintained and FIML typically produces less biased results than listwise deletion (Enders 2010).

Results

Descriptive statistics

Table 1 shows manifest correlations, minima, maxima, means, and standard deviations for all variables. Bivariate correlations were found between variables of interest, of which most appeared to be highly significant. All predictor and outcome variables correlated positively with each other, showing that ML was associated with academic achievement in different school domains 4 years later. Moreover, the correlations among predictors support our assumption that calculation skills, mathematical self-concept, reading comprehension, and reasoning need to be studied together. With respect to control variables, gender differences were found for all variables except SES, ICT literacy, and reasoning in Grade 9. Male students scored higher on all variables except listening comprehension in Grade 9 and reading comprehension in Grades 5 and 9, on which female students scored higher. This finding indicates that gender is an important control variable for our analyses. For all variables of interest apart from mathematical self-concept, significant correlations with SES were found, with higher SES students scoring higher on all measures.

Table 1 Manifest correlations of mathematical literacy, math grade, mathematical self-concept, information and communication technology (ICT) literacy, scientific literacy, reading comprehension, listening comprehension, reasoning, socioeconomic status (SES), and gender; minima, maxima, means, and standard deviations of all variables

Full size table

Structural equation model

As our descriptive statistics indicate, ML was associated with later academic achievement in different school domains (research question 1). Furthermore, predictors of ML were correlated with each other, implying that they should be studied together (research question 2). To explore our hypotheses about controlling for prior achievement in the respective domain when looking for predictive effects of ML on achievement in different domains (hypothesis 1) and studying predictors comprehensively (hypothesis 2), we calculated a structural equation model. The estimated model is presented in Fig. 1. Since, as expected, we did not find math grade and mathematical self-concept to significantly add to later achievement in school domains other than ML when controlling for prior achievement, we did not include corresponding paths in the model. We found significant covariances for all exogenous variables (values are not depicted in Fig. 1 for better readability). For better readability of the figure, the corresponding path coefficients for our regression analyses are presented in Table 2. Given skewness ranging from − 1.12 (reasoning) to 0.63 (math grade) and kurtosis ranging from − 0.69 (mathematical self-concept) to 1.21 (reasoning), normal distribution of the data was assumed (cf., Kaplan 2009). The model produced a good fit of the data (cf., Hu and Bentler 1999), with RMSEA = .035, CFI = .998, and TLI = .982.

Fig. 1

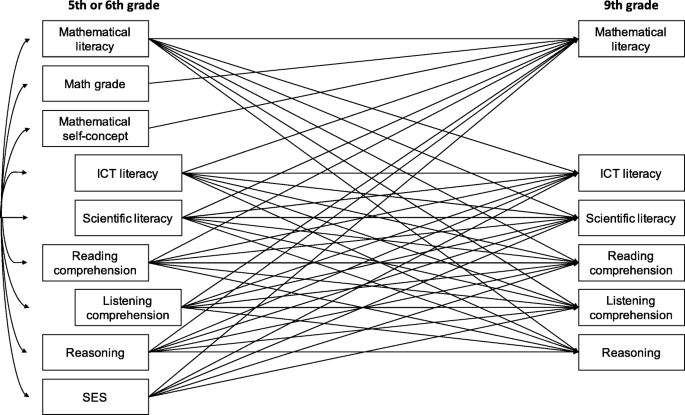
Estimated model without coefficients. Root mean square error of approximation = .035, comparative fit index = .998, Tucker–Lewis index = .982. ICT = information and communication technology; SES = socioeconomic status. On the left, ICT literacy, scientific literacy, and listening comprehension from Grade 6 (indented), math grade from Grade 4, others from Grade 5. Paths for the effect of math grade and mathematical self-concept on later achievement in school domains other than mathematical literacy were not included because no significant effects were found

Full size image

Table 2 Standardized path coefficients (β) of the structural equation model in Fig. 1

Full size table

As we wanted to investigate only the effects of ML on later academic achievement while controlling for prior achievement in the respective domain (research question 1), we did not need to predict mathematical self-concept in Grade 9. While math grade was used as a predictor in terms of students' basic calculation skills in Grade 5, we did not include students' math grade as an outcome variable in Grade 9. Moreover, SES was assessed in Grade 5 and was used as a control variable, which is why we did not include SES in Grade 9 in the model. To account for the nested structure of the data, we tested for models with values centered around schoolhouse as well as classroom means but found no changes in the significances of path coefficients.

As we found bivariate correlations with gender for several variables, we estimated a multigroup model to test for gender differences. No significant gender differences were found for loadings or path coefficients when testing for differences in model fit indices among different models. Regarding our minor hypothesis on gender effects, we conclude that analyses with respect to our other hypotheses are valid since we did not find any gender differences. We also tested for different models with paths regarding influences of SES on later reasoning but did not find a significant effect.

Research question 1: impact of ML on academic achievement

Our model revealed significant path coefficients from ML in Grade 5 to achievement in four school domains and reasoning in Grade 9 while considering prior achievement in the respective domain. First, on ICT literacy in Grade 9 (R ² = .54 for all predictors), a significant effect (β = .19) of ML was found. Second, a significant path coefficient (β = .17) was found from ML in Grade 5 to scientific literacy in Grade 9 (R ² = .57). Third, for reading comprehension in Grade 9 (R ² = .49), a significant path coefficient (β = .06) was found from ML in Grade 5. Fourth, a significant path coefficient of β = .09 was found from ML in Grade 5 to listening comprehension in Grade 9 (R ² = .42). Fifth, regarding reasoning in Grade 9 (R ² = .33), a significant path coefficient (β = .23) was found from ML in Grade 5. Prior achievement in other domains showed no significant effects on reasoning in Grade 9, apart from scientific literacy, for which there was also a significant path coefficient (β = .10). Though we did not make assumptions on the effects of ML on reasoning, ML was found to impact reasoning 4 years later, while prior achievements in other domains except scientific literacy did not have a significant effect on later reasoning. Moreover, significant paths were found for SES to later academic achievement in different school domains except for ICT literacy, confirming the importance of SES as a control variable. Our results confirm hypothesis 1, showing that ML predicted achievement in different school domains 4 years later when prior achievement in the respective domain was taken into account. This provides evidence for the presumed transfer effect of ML on achievement in other school domains over time.

Research question 2: predictors of ML

Significant paths were found for all assumed predictors on ML in Grade 9, namely math grade, mathematical self-concept, prior achievement in different domains (i.e., ICT literacy, scientific literacy, reading, and listening comprehension), reasoning, and SES with the autoregressive path showing the highest effect (β = .35). The regression analysis explained 60% of the variance in ML in Grade 9. This finding confirms hypothesis 2, supporting the assumption that predictors found in previous studies still have an effect on ML throughout the secondary school years even if predictive effects among them and prior achievement in ML and other domains are accounted for. This supports taking an integrative view of predictor variables when investigating ML.

Discussion

The main goal of this study was to examine transfer effects of ML on later academic achievement in different school domains (i.e., ICT literacy, scientific literacy, reading comprehension, and listening comprehension) while taking known predictors into account and considering prior achievement in the respective domain, SES, and gender. In an extension to previous research, we focused on ML across the secondary school years using representative longitudinal data from the NEPS (Blossfeld et al. 2011).

Consistent with our hypotheses, we found effects of ML on later academic achievement in different domains. These results confirm our hypotheses regarding the influence of ML on achievement in different school domains in terms of a transfer effect. In line with previous findings from Baumert et al. (2012), Chu et al. (2016), and Korpipää et al. (2017), we suggest that the transfer effect of ML is due to the promotion of domain-general abilities such as problem-solving and a deeper understanding of texts, realistic contexts, and students' everyday life through competence development linked with students' ML. We even found a significant effect of ML in Grade 5 on reasoning in Grade 9—while controlling for prior reasoning—which strengthens this explanation.

In line with current research on predictors of ML, our study confirmed the role of calculation skills, mathematical self-concept, reading comprehension, and reasoning as predictive factors of ML (Andersson 2007; Baumert et al. 2007; Borromeo Ferri 2006; Chu et al. 2016; Kriegbaum et al. 2015; Pajares and Miller 1994). We assumed these predictors, found in separate studies to have an effect on ML, to predict later ML when examined at the same time and while controlling for prior achievement. Our results support an integrative view of different phases of the process of solving mathematical problems, as has been suggested in various theoretical articles and qualitative studies (e.g., Kaiser et al. 2015; Leiss and Tropper 2014). Concerning cognitive models of ML, which typically view the process of solving mathematical problems as consisting of different phases, our results reveal that mathematical self-concept still has an effect on ML when prior achievement is controlled for. This is in line with findings from Marsh et al. (2005) and self-enhancement models of self-concept (Bandura 1997), which suggest there is an underlying motivational basis to the effects of mathematical self-concept on ML. Students profit from high self-concept because it enhances their motivation, which is especially useful when attempting the complex tasks involved in ML. We found that reasoning also showed an effect on later ML, which is in accordance with previous arguments on the role of cognitive skills in ML (Baumert et al. 2007) and underlines the role of general cognitive abilities, in the sense of shared skill sets of ML and achievement in other domains.

In contrast to what previous research showed (e.g., Robinson and Lubienski 2011), we found no gender differences in paths from comprehensive predictors to ML or from ML, prior achievement, and reasoning to achievement in different school domains. We presume that this may be due to our operationalization of outcome variables as competence measures (in contrast to GPA) and the fact that taking other explanatory variables such as math grade or self-concept into account may diminish gender effects.

Regarding SES, we found significant paths to ML and achievement in different school domains 4 years later, which is in line with previous research on achievement measures (Sirin 2005). Though an SES-related achievement gap appears to narrow through the course of secondary school (Caro and Lehmann 2009), students with higher SES still score higher on different achievement measures in Grade 9.

Limitations and directions for future research

We examined the influence of ML on later academic achievement longitudinally throughout secondary school with a national representative sample. While this is an important time span previously neglected in studies on ML, a longer time span reaching into students' vocational years would shed light on further academic as well as nonacademic outcomes.

Because we used data from the large-scale NEPS assessments, limitations lie in the restriction to scales used in the study. Mathematical self-concept, for instance, while having the strength of being domain specific (Schöber et al. 2018), consisted of only three items. Broader and more differentiating concepts such as self-efficacy, attitudes, or motivational variables would be interesting to take into account to cover self-concept. Especially the role of self-efficacy in ML would appear to warrant further attention (Krawitz and Schukajlow 2017; Schukajlow et al. 2012). With respect to cognitive skills, which have been argued and empirically found to play an important role in mathematical problem-solving, the domain of verbal intelligence should be examined as well, because reading and listening comprehension were found to influence ML.

Disregarded by our research approach were other phases in the cognitive process of ML, such as metacognitive skills (Maass 2006), working memory (Swanson 2011), and personality (Phonapichat et al. 2014), all argued to have an influence on solving mathematical problems. Concerning individual differences in competence development, differences regarding migration background are a broadly discussed topic in the current literature. With controlling for SES, we have partly addressed this issue because SES is considered to be linked to migration background (e.g., Lenkeit et al. 2015). Future studies should address the influence of migration background directly to broaden the integrative view of predictive factors of ML, as differences in mathematical development were found to be entangled with reading competence (e.g., Lehner et al. 2017).

From a methodological perspective, though our results are longitudinal, they are restricted in that they are not interventional. Besides this, the possibility of there being other paths that were not analyzed restricts the validity of causal effects. The argument for causal transfer effects of ML on achievement in different school domains relies on theoretical assumptions (i.e., shared skill sets being fostered by gains in ML) and is methodologically strengthened by controlling for prior achievement in the respective domains as well as taking ML 4 years previous into account. Nevertheless, we only tested for predictive patterns, resulting in the need for experimental manipulations (e.g., instructional approaches to teaching ML) to get more evidence of causal transfer effects. Moreover, with respect to other scholars, Leiss et al. (2010) argued that addressing how teachers themselves are taught to foster their students' ML is essential. Lehner et al. (2017) postulated encouraging, motivating lessons, classroom management, and schooling structure to be central for mathematical competence development. Applying a solution plan when solving mathematical problems could foster ML as well as mathematical self-efficacy (Schukajlow et al. 2015). Also, class sizes seem to play a role, though findings are still inconclusive (Ehrenberg et al. 2001; Hattie 2009; Schukajlow and Blum 2011). To enlarge the integrative view, interventional studies are needed to further investigate ML and its role in achievement and life success.

Conclusion and practical implications

We found consistent support for the importance of ML for general academic achievement. ML was found to be linked with achievement in math-related domains (ICT literacy, scientific literacy) as well as domains not directly related to mathematics (listening and reading comprehension). We argue that this not only underlines the effect of ML on understanding mathematics in today's life contexts (Baumert et al. 2007) but also indicates the existence of a transfer effect of applying this understanding for better life competence in domains other than mathematics. In our view, this means that students profit—in terms of their future academic achievement—when educators and policy makers invest in students' ML. Our results suggest that the success of such investment is comparable with that obtained by the investment in fostering other competences such as reading comprehension. The universality of our model regarding gender differences reinforces the idea of not differentiating between boys and girls concerning the support they get in learning mathematics and reading.

The consistent support we found in line with previous studies regarding the influence of predictive factors on ML could encourage teachers and parents to foster students' mathematical self-concept as well as their ML from early on. This also supports the current directions in international educational standards to implement the literacy perspective in the domain of mathematics in the conceptualizations of school curricula (National Council of Teachers of Mathematics 2003; Standing Conference of the Ministers of Education and Cultural Affairs of the Federal Republic of Germany 2004). Given our findings and following the ML concept of PISA 2021 (OECD 2019), teachers should, when designing their mathematics lessons and motivating their students, keep in mind the applicability for current and post-school participation in a culture. The theoretical insights and evidence of our study indicate that making ML part of a daily routine elicits mathematical development and trains skills that advance students in other school domains. We assume that this different perspective on ML leads to a deeper, broadened understanding of the significance of mathematics in students' everyday lives. Keeping in mind the relationships of reasoning and self-concept as well as the links between SES and ML, we strongly suggest integrating encouraging, vivid, and resource-based teaching methods that foster students' mathematical self-concept when guiding students to tackle the challenging elements of ML problems. Applying a solution plan (Schukajlow et al. 2015) might prove to be useful in this regard. Following these recommendations, we are convinced that ML is key to motivating a diverse range of students. Finally, the impact we found of SES on later achievement in different school domains when controlling for prior achievement highlights the need for educational equity.

Notes

1. 1.

   COACTIV is the abbreviation for the Professional Competence of Teachers, Cognitively Activating Instruction, and Development of Students' Mathematical Literacy project.

References

1. Andersson, U. (2007). The contribution of working memory to children's mathematical word problem solving. Applied Cognitive Psychology, 21(9), 1201–1216. https://doi.org/10.1002/acp.1317.

   Article  Google Scholar

2. Arán Filippetti, V., & Richaud, M. C. (2016). A structural equation modeling of executive functions, IQ and mathematical skills in primary students: differential effects on number production, mental calculus and arithmetical problems. Child Neuropsychology, 23, 1–25. https://doi.org/10.1080/09297049.2016.1199665.

   Article  Google Scholar

3. Aunola, K., Leskinen, E., Lerkkanen, M.-K., & Nurmi, J.-E. (2004). Developmental dynamics of math performance from preschool to grade 2. Journal of Educational Psychology, 96(4), 699–713. https://doi.org/10.1037/0022-0663.96.4.699.

   Article  Google Scholar

4. Bandura, A. (1997). Self-efficacy: the exercise of control. New York: W.H. Freeman.

   Google Scholar

5. Baumert, J., Brunner, M., Lüdtke, O., & Trautwein, U. (2007). Was messen internationale Schulleistungsstudien?—Resultate kumulativer Wissenserwerbsprozesse. Psychologische Rundschau, 58(2), 118–145. https://doi.org/10.1026/0033-3042.58.2.118.

   Article  Google Scholar

6. Baumert, J., Nagy, G., & Lehmann, R. (2012). Cumulative advantages and the emergence of social and ethnic inequality: Matthew effects in reading and mathematics development within elementary schools? Child Development, 83(4), 1347–1367. https://doi.org/10.1111/j.1467-8624.2012.01779.x.

   Article  Google Scholar

7. Best, J. R., Miller, P. H., & Naglieri, J. A. (2011). Relations between executive function and academic achievement from ages 5 to 17 in a large, representative national sample. Learning and Individual Differences, 21(4), 327–336. https://doi.org/10.1016/j.lindif.2011.01.007.

   Article  Google Scholar

8. Blomhoj, M., & Jensen, T. H. (2003). Developing mathematical modelling competence: conceptual clarification and educational planning. Teaching Mathematics and Its Applications, 22(3), 123–139. https://doi.org/10.1093/teamat/22.3.123.

   Article  Google Scholar

9. Blossfeld, H.-P., Roßbach, H.-G., & von Maurice, J. (2011). Editorial. Zeitschrift für Erziehungswissenschaft, 14(Suppl. 2), 1–4. https://doi.org/10.1007/s11618-011-0198-z.

   Article  Google Scholar

10. Blum, W., & Borromeo Ferri, R. (2009). Mathematical modelling: can it be taught and learnt? Journal of Mathematical Modelling and Application, 1(1), 45–58.

    Google Scholar

11. Blum, W., Neubrand, M., Ehmke, T., Senkbeil, M., Jordan, A., Ulfig, F., & Carstensen, C. H. (2004). Mathematische Kompetenz. In M. Prenzel, J. Baumert, W. Blum, R. Lehmann, D. Leutner, M. Neubrand, et al. (Eds.), PISA 2003. Der Bildungsstand der Jugendlichen in Deutschland—Ergebnisse des zweiten internationalen Vergleichs (pp. 47–92). Waxmann: Münster.

    Google Scholar

12. Borromeo Ferri, R. (2006). Theoretical and empirical differentiations of phases in the modelling process. Zentralblatt der Mathematikdidaktik, 38(2), 86–95. https://doi.org/10.1007/BF02655883.

    Article  Google Scholar

13. Brauns, H., Scherer, S., & Steinmann, S. (2003). The CASMIN educational classification in international comparative research. In J. H. P. Hoffmeyer-Zlotnik & C. Wolf (Eds.), Advances in cross-national comparison: a European working book for demographic and socio-economic variables (pp. 221–244). Boston: Springer.

    Chapter  Google Scholar

14. Brown, J. P., & Stillman, G. A. (2017). Developing the roots of modelling conceptions: 'mathematical modelling is the life of the world'. International Journal of Mathematical Education in Science and Technology, 48(3), 353–373. https://doi.org/10.1080/0020739X.2016.1245875.

    Article  Google Scholar

15. Brunner, M., Lang, F. R., & Lüdtke, O. (2014). Erfassung der fluiden kognitiven Leistungfähigkeit über die Lebensspanne im Rahmen der National Educational Panel Study: Expertise (NEPS Working Paper No. 42). Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study.

16. Caro, D. H., & Lehmann, R. (2009). Achievement inequalities in Hamburg schools: how do they change as students get older? School Effectiveness and School Improvement, 20(4), 407–431. https://doi.org/10.1080/09243450902920599.

    Article  Google Scholar

17. Chu, F. W., van Marle, K., & Geary, D. C. (2016). Predicting children's reading and mathematics achievement from early quantitative knowledge and domain-general cognitive abilities. Frontiers in Psychology. https://doi.org/10.3389/fpsyg.2016.00775.

18. DiPrete, T. A., & Eirich, G. M. (2006). Cumulative advantage as a mechanism for inequality: a review of theoretical and empirical developments. Annual Review of Sociology, 32(1), 271–297. https://doi.org/10.1146/annurev.soc.32.061604.123127.

    Article  Google Scholar

19. Duchhardt, C., & Gerdes, A. (2012). NEPS technical report for mathematics—scaling results of Starting Cohort 3 in fifth grade (NEPS Working Paper No. 19). Bamberg: Otto Friedrich University, National Educational Panel Study.

20. Duncan, G. J., Dowsett, C. J., Claessens, A., Magnuson, K., Huston, A. C., Klebanov, P., et al. (2007). School readiness and later achievement. Developmental Psychology, 43(6), 1428–1446. https://doi.org/10.1037/0012-1649.43.6.1428.

    Article  Google Scholar

21. Ehmke, T., Wild, E., & Müller-Kalhoff, T. (2005). Comparing adult mathematical literacy with PISA students: results of a pilot study. ZDM, 37(3), 159–167.

    Google Scholar

22. Ehrenberg, R. G., Brewer, D. J., Gamoran, A., & Willms, J. D. (2001). Class size and student achievement. Psychological Science in the Public Interest, 2(1), 1–30. https://doi.org/10.1111/1529-1006.003.

    Article  Google Scholar

23. Ehrtmann, L., & Wolter, I. (2018). The impact of students' gender-role orientation on competence development in mathematics and reading in secondary school. Learning and Individual Differences, 61, 256–264. https://doi.org/10.1016/j.lindif.2018.01.004.

    Article  Google Scholar

24. Enders, C. K. (2010). Applied missing data analysis. New York: The Guilford Press.

    Google Scholar

25. English, L. D., & Watters, J. J. (2005). Mathematical modelling in the early school years. Mathematics Education Research Journal, 16(3), 58–79.

    Article  Google Scholar

26. Fabian, P., Goy, M., Jarsinski, S., Naujokat, K., Prosch, A., Strietholt, R., et al. (2019). Transition and development from lower secondary to upper secondary school. In H.-P. Blossfeld & H.-G. Roßbach (Eds.), Education as a lifelong process (Vol. 3, pp. 231–252). Wiesbaden: Springer. https://doi.org/10.1007/978-3-658-23162-0_13.

    Chapter  Google Scholar

27. Fischer, L., Rohm, T., Gnambs, T., & Carstensen, C. H. (2016). Linking the data of the competence tests (NEPS Survey Paper No. 1). Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study.

28. Fuchs, L. S., Fuchs, D., Compton, D. L., Powell, S. R., Seethaler, P. M., Capizzi, A. M., et al. (2006). The cognitive correlates of third-grade skill in arithmetic, algorithmic computation, and arithmetic word problems. Journal of Educational Psychology, 98(1), 29–43. https://doi.org/10.1037/0022-0663.98.1.29.

    Article  Google Scholar

29. Funke, L., Kähler, J., & Hahn, I. (2016). NEPS technical report for science: scaling results of Starting Cohort 3 in 6th grade (NEPS Survey Paper No. 5). Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study.

30. Geary, D. C. (2011). Cognitive predictors of achievement growth in mathematics: a 5-year longitudinal study. Developmental Psychology, 47(6), 1539–1552. https://doi.org/10.1037/a0025510.

    Article  Google Scholar

31. Gehrer, K., Zimmermann, S., Artelt, C., & Weinert, S. (2013). NEPS framework for assessing reading competence and results from an adult pilot study. Journal for Educational Research Online, 5(2), 50–79.

    Google Scholar

32. Grimm, K. J. (2008). Longitudinal associations between reading and mathematics achievement. Developmental Neuropsychology, 33(3), 410–426. https://doi.org/10.1080/87565640801982486.

    Article  Google Scholar

33. Gut, J., Reimann, G., & Grob, A. (2012). Kognitive, sprachliche, mathematische und sozial-emotionale Kompetenzen als Prädiktoren späterer schulischer Leistungen: Können die Leistungen eines Kindes in den IDS dessen Schulleistungen drei Jahre später vorhersagen? Zeitschrift für Pädagogische Psychologie, 26(3), 213–220. https://doi.org/10.1024/1010-0652/a000070.

34. Haberkorn, K., & Pohl, S. (2013). Cognitive basic skills—data in the scientific use file. Bamberg: University of Bamberg, National Educational Panel Study.

    Google Scholar

35. Hahn, I., Schöps, K., Rönnebeck, S., Martensen, M., Hansen, S., Sass, S., et al. (2013). Assessing scientific literacy over the lifespan—a description of the NEPS science framework and the test development. Journal for Educational Research Online, 5(2), 110–138.

    Google Scholar

36. Hattie, J. A. C. (2009). Visible learning: a synthesis of over 800 meta-analyses relating to achievement. London: Routledge.

    Google Scholar

37. Hecker, K., Südkamp, A., Leser, C., & Weinert, S. (2015). Entwicklung eines Tests zur Erfassung von Hörverstehen auf Textebene bei Schülerinnen und Schülern der Klassenstufe 9 (NEPS Working Paper No. 53). Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study.

38. Hoffman, B., & Spatariu, A. (2008). The influence of self-efficacy and metacognitive prompting on math problem-solving efficiency. Contemporary Educational Psychology, 33(4), 875–893. https://doi.org/10.1016/j.cedpsych.2007.07.002.

    Article  Google Scholar

39. Hu, L., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6(1), 1–55. https://doi.org/10.1080/10705519909540118.

    Article  Google Scholar

40. Hwang, J., & Riccomini, P. J. (2016). Enhancing mathematical problem solving for secondary students with or at risk of learning disabilities: a literature review. Learning Disabilities Research & Practice, 31(3), 169–181. https://doi.org/10.1111/ldrp.12105.

    Article  Google Scholar

41. Jensen, T. H. (2007). Assessing mathematical modelling competency. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical modelling (ICTMA12) Education, engineering and economics (pp. 510–517). Chichester: Horwood.

    Google Scholar

42. Jordan, N. C., Kaplan, D., & Hanich, L. B. (2002). Achievement growth in children with learning difficulties in mathematics: findings of a two-year longitudinal study. Journal of Educational Psychology, 94(3), 586–597. https://doi.org/10.1037//0022-0663.94.3.586.

    Article  Google Scholar

43. Kaiser, G., Blum, W., Borromeo Ferri, R., & Greefrath, G. (2015). Anwendungen und Modellieren. In R. Bruder, L. Hefendehl-Hebeker, B. Schmidt-Thieme, & H.-G. Weigand (Eds.), Handbuch der Mathematikdidaktik (pp. 357–383). Berlin: Springer. https://doi.org/10.1007/978-3-642-35119-8_13.

    Chapter  Google Scholar

44. Kaplan, D. (2009). Structural equation modeling: foundations and extensions (2nd ed.). Thousand Oaks: Sage Publications. https://doi.org/10.4135/9781452226576.

    Book  Google Scholar

45. Kiemer, K., Haag, N., Müller, K., & Ehmke, T. (2017). Einfluss sozialer und zuwanderungsbezogener Disparitäten, sowie der Klassenkomposition auf die Veränderung der mathematischen Kompetenz von der neunten zur zehnten Klassenstufe. Zeitschrift für Erziehungswissenschaft, 20(Suppl. 2), 125–149. https://doi.org/10.1007/s11618-017-0753-3.

    Article  Google Scholar

46. Korpipää, H., Koponen, T., Aro, M., Tolvanen, A., Aunola, K., Poikkeus, A.-M., et al. (2017). Covariation between reading and arithmetic skills from Grade 1 to Grade 7. Contemporary Educational Psychology, 51, 131–140. https://doi.org/10.1016/j.cedpsych.2017.06.005.

    Article  Google Scholar

47. Krawitz, J., & Schukajlow, S. (2017). Do students value modelling problems, and are they confident they can solve such problems? Value and self-efficacy for modelling, word, and intra-mathematical problems. ZDM, 50, 143–157. https://doi.org/10.1007/s11858-017-0893-1.

    Article  Google Scholar

48. Kriegbaum, K., Jansen, M., & Spinath, B. (2015). Motivation: a predictor of PISA's mathematical competence beyond intelligence and prior test achievement. Learning and Individual Differences, 43, 140–148. https://doi.org/10.1016/j.lindif.2015.08.026.

    Article  Google Scholar

49. Kuger, S., Klieme, E., Lüdtke, O., Schiepe-Tiska, A., & Reiss, K. (2017). Mathematikunterricht und Schülerleistung in der Sekundarstufe: Zur Validität von Schülerbefragungen in Schulleistungsstudien. Zeitschrift für Erziehungswissenschaft, 20(Suppl. 2), 61–98. https://doi.org/10.1007/s11618-017-0750-6.

    Article  Google Scholar

50. Kunter, M., Baumert, J., Blum, W., Klusmann, U., Krauss, S., & Neubrand, M. (2013). Cognitive activation in the mathematics classroom and professional competence of teachers: results from the COACTIV Project. New York: Springer.

    Book  Google Scholar

51. Lee, K., Ng, S.-F., Ng, E.-L., & Lim, Z.-Y. (2004). Working memory and literacy as predictors of performance on algebraic word problems. Journal of Experimental Child Psychology, 89(2), 140–158. https://doi.org/10.1016/j.jecp.2004.07.001.

    Article  Google Scholar

52. Lehmann, R., & Nikolova, R. (2007). Element: Erhebung zum Lese-und Mathematikverständnis. Entwicklungen in den Jahrgangsstufen 4 bis 6 in Berlin. Berlin: Senate Department for Education, Youth and Sport.

53. Lehner, M. C., Heine, J.-H., Sälzer, C., Reiss, K., Haag, N., & Heinze, A. (2017). Veränderung der mathematischen Kompetenz von der neunten zur zehnten Klassenstufe. Zeitschrift für Erziehungswissenschaft, 20(Suppl. 2), 7–36. https://doi.org/10.1007/s11618-017-0746-2.

    Article  Google Scholar

54. Leiss, D., & Tropper, N. (2014). Mathematisches Modellieren. In D. Leiss & N. Tropper, Umgang mit Heterogenität im Mathematikunterricht (pp. 23–36). https://doi.org/10.1007/978-3-642-45109-6_3.

55. Leiss, D., Schukajlow, S., Blum, W., Messner, R., & Pekrun, R. (2010). The role of the situation model in mathematical modelling—task analyses, student competencies, and teacher interventions. Journal für Mathematik-Didaktik, 31(1), 119–141. https://doi.org/10.1007/s13138-010-0006-y.

    Article  Google Scholar

56. Lekholm, A. K., & Cliffordson, C. (2008). Discrepancies between school grades and test scores at individual and school level: effects of gender and family background. Educational Research and Evaluation, 14(2), 181–199. https://doi.org/10.1080/13803610801956663.

    Article  Google Scholar

57. Lenkeit, J., Caro, D. H., & Strand, S. (2015). Tackling the remaining attainment gap between students with and without immigrant background: an investigation into the equivalence of SES constructs. Educational Research and Evaluation, 21(1), 60–83. https://doi.org/10.1080/13803611.2015.1009915.

    Article  Google Scholar

58. Leutner, D., Fleischer, J., Wirth, J., Greiff, S., & Funke, J. (2012). Analytische und dynamische Problemlösekompetenz im Lichte internationaler Schulleistungsvergleichsstudien: Untersuchungen zur Dimensionalität. Psychologische Rundschau, 63(1), 34–42. https://doi.org/10.1026/0033-3042/a000108.

    Article  Google Scholar

59. Maass, K. (2006). What are modelling competencies? Zentralblatt für Didaktik der Mathematik, 38(2), 113–142.

    Article  Google Scholar

60. Marsh, H. W., Trautwein, U., Lüdtke, O., Köller, O., & Baumert, J. (2005). Academic self-concept, interest, grades, and standardized test scores: reciprocal effects models of causal ordering. Child Development, 76(2), 397–416. https://doi.org/10.1111/j.1467-8624.2005.00853.x.

    Article  Google Scholar

61. Mullis, V. S., Martin, M. O., Ruddock, G. J., O'Sullivan, C. Y., & Preuschoff, C. (2009). TIMSS 2011 assessment frameworks. Chestnut Hill, MA: TIMSS & PIRLS International Study Center.

    Google Scholar

62. National Council of Teachers of Mathematics. (2003). Principles and standards for school mathematics (3rd ed.). Reston: Author.

    Google Scholar

63. Neumann, I., Duchhardt, C., Grüssing, M., Heinze, A., Knopp, E., & Ehmke, T. (2013). Modeling and assessing mathematical competence over the lifespan. Journal for Educational Research Online, 5(2), 80–109.

    Google Scholar

64. Organisation for Economic Co-operation and Development. (2003). The PISA 2003 assessment framework: mathematics, reading, science and problem-solving knowledge and skills. Paris: Author.

    Google Scholar

65. Organisation for Economic Co-operation and Development. (2013). PISA 2012 assessment and analytical framework: mathematics, reading, science, problem solving and financial literacy. Paris: Author.

    Google Scholar

66. Organisation for Economic Co-operation and Development. (2019). PISA 2018 Results (Volume I): what students know and can do. https://doi.org/10.1787/5f07c754-en

67. Pajares, F., & Miller, M. D. (1994). Role of self-efficacy and self-concept beliefs in mathematical problem solving: a path analysis. Journal of Educational Psychology, 86(2), 193–203. https://doi.org/10.1037/0022-0663.86.2.193.

    Article  Google Scholar

68. Pape, S. J., & Wang, C. (2003). Middle school children's strategic behavior: classification and relation to academic achievement and mathematical problem solving. Instructional Science, 31, 419–449. https://doi.org/10.1023/A:1025710707285.

    Article  Google Scholar

69. Phonapichat, P., Wongwanich, S., & Sujiva, S. (2014). An analysis of elementary school students' difficulties in mathematical problem solving. Procedia—Social and Behavioral Sciences, 116, 3169–3174. https://doi.org/10.1016/j.sbspro.2014.01.728.

    Article  Google Scholar

70. Pohl, S., & Carstensen, C. H. (2012). NEPS technical report—scaling the data of the competence tests (NEPS Working Paper No. 14). Bamberg: Otto Friedrich University, National Educational Panel Study.

71. Pohl, S., & Carstensen, C. H. (2013). Scaling of competence tests in the National Educational Panel Study—many questions, some answers, and further challenges. Journal for Educational Research Online, 5(2), 189–216.

    Google Scholar

72. Pohl, S., Haberkorn, K., Hardt, K., & Wiegand, E. (2012). NEPS technical report for reading—scaling results of Starting Cohort 3 in fifth grade (NEPS Working Paper No. 15). Bamberg: Otto Friedrich University, National Educational Panel Study.

73. Pohl, S., Haberkorn, K., & Carstensen, C. H. (2015). Measuring competencies across the lifespan—challenges of linking test scores. In M. Stemmler, A. von Eye, & W. Wiedermann (Eds.), Dependent data in social sciences research (Springer) proceedings in mathematics & statistics (Vol. 145, pp. 281–308). Cham: Springer International. https://doi.org/10.1007/978-3-319-20585-4_12.

    Chapter  Google Scholar

74. Preckel, F., Goetz, T., Pekrun, R., & Kleine, M. (2008). Gender differences in gifted and average-ability students: comparing girls' and boys' achievement, self-concept, interest, and motivation in mathematics. Gifted Child Quarterly, 52(2), 146–159. https://doi.org/10.1177/0016986208315834.

    Article  Google Scholar

75. Prenzel, M. (2006). Untersuchungen zur Kompetenzentwicklung im Verlauf eines Schuljahres: Die Ergebnisse von PISA-I-Plus im Überblick. In M. Prenzel, J. Baumert, W. Blum, R. Lehmann, D. Leutner, M. Neubrand, et al. (Eds.), PISA 2003. Untersuchungen zur Kompetenzentwicklung im Verlauf eines Schuljahres (pp. 15–27). Waxmann: Münster.

    Google Scholar

76. R Development Core Team. (2008). R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing.

    Google Scholar

77. Robinson, J. P., & Lubienski, S. T. (2011). The development of gender achievement gaps in mathematics and reading during elementary and middle school: examining direct cognitive assessments and teacher ratings. American Educational Research Journal, 48(2), 268–302. https://doi.org/10.3102/0002831210372249.

    Article  Google Scholar

78. Rohm, T., Freund, M., Gnambs, T., & Fischer, L. (2017). NEPS technical report for listening comprehension: scaling results of Starting Cohort 3 for Grade 9 (NEPS Survey Paper No. 21). Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study.

79. Roßbach, H.-G., Tietze, W., & Weinert, S. (2005). Peabody Picture Vocabulary Test—Revised. Deutsche Forschungsversion des Tests von L. M. Dunn & L. M. Dunn von 1981. Bamberg: Free University of Berlin.

    Google Scholar

80. Scharl, A., Fischer, L., Gnambs, T., & Rohm, T. (2017). NEPS technical report for reading: scaling results of Starting Cohort 3 for Grade 9 (NEPS Survey Paper No. 20). Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study.

81. Schnittjer, I., & Duchhardt, C. (2015). Mathematical competence: framework and exemplary test items. Bamberg: Leibniz Institute for Educational Trajectories.

    Google Scholar

82. Schöber, C., Schütte, K., Köller, O., McElvany, N., & Gebauer, M. M. (2018). Reciprocal effects between self-efficacy and achievement in mathematics and reading. Learning and Individual Differences, 63, 1–11. https://doi.org/10.1016/j.lindif.2018.01.008.

    Article  Google Scholar

83. Schommer-Aikins, M., Duell, O. K., & Hutter, R. (2005). Epistemological beliefs, mathematical problem-solving beliefs, and academic performance of middle school students. The Elementary School Journal, 105(3), 289–304. https://doi.org/10.1086/428745.

    Article  Google Scholar

84. Schukajlow, S., & Blum, W. (2011). Zum Einfluss der Klassengröße auf Modellierungskompetenz, Selbst- und Unterrichtswahrnehmungen von Schülern in selbständigkeitsorientierten Lehr-Lernformen. Journal für Mathematik-Didaktik, 32(2), 133–151. https://doi.org/10.1007/s13138-011-0025-3.

    Article  Google Scholar

85. Schukajlow, S., Leiss, D., Pekrun, R., Blum, W., Müller, M., & Messner, R. (2012). Teaching methods for modelling problems and students' task-specific enjoyment, value, interest and self-efficacy expectations. Educational Studies in Mathematics, 79(2), 215–237. https://doi.org/10.1007/s10649-011-9341-2.

    Article  Google Scholar

86. Schukajlow, S., Kolter, J., & Blum, W. (2015). Scaffolding mathematical modelling with a solution plan. ZDM, 47(7), 1241–1254. https://doi.org/10.1007/s11858-015-0707-2.

    Article  Google Scholar

87. Senkbeil, M., & Ihme, J. M. (2017). NEPS technical report for computer literacy: scaling results of Starting Cohort 3 for Grade 9 (NEPS Survey Paper No. 29). Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study.

88. Senkbeil, M., Ihme, J. M., & Adrian, E. D. (2014). NEPS technical report for computer literacy: scaling results of Starting Cohort 3 in Grade 6 (Wave 2) (NEPS Working Paper No. 39). Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study.

89. Siegler, R. S., Duncan, G. J., Davis-Kean, P. E., Duckworth, K., Claessens, A., Engel, M., et al. (2012). Early predictors of high school mathematics achievement. Psychological Science, 23(7), 691–697. https://doi.org/10.1177/0956797612440101.

    Article  Google Scholar

90. Sirin, S. R. (2005). Socioeconomic status and academic achievement: a meta-analytic review of research. Review of Educational Research, 75(3), 417–453. https://doi.org/10.3102/00346543075003417.

    Article  Google Scholar

91. Sokolowski, A. (2015). The effects of mathematical modelling on students' achievement—meta-analysis of research. IAFOR Journal of Education, 3(1), 93–114.

    Article  Google Scholar

92. Standing Conference of the Ministers of Education and Cultural Affairs of the Federal Republic of Germany. (2004). Bildungsstandards im Fach Mathematik für den Mittleren Schulabschluss (Grade 10). Neuwied: Luchterhand.

    Google Scholar

93. Swanson, H. L. (2011). Working memory, attention, and mathematical problem solving: a longitudinal study of elementary school children. Journal of Educational Psychology, 103(4), 821–837. https://doi.org/10.1037/a0025114.

    Article  Google Scholar

94. Swanson, H. L., Jerman, O., & Zheng, X. (2008). Growth in working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. Journal of Educational Psychology, 100(2), 343–379. https://doi.org/10.1037/0022-0663.100.2.343.

    Article  Google Scholar

95. United Nations Educational, Scientific and Cultural Organization Institute for Statistics. (2013). ISCED 2011: International Standard Classification of Education. Montreal: UNESCO.

    Google Scholar

96. Van den Ham, A.-K., Schnittjer, I., & Gerken, A.-L. (2018). NEPS technical report for mathematics: scaling results of Starting Cohort 3 for Grade 9 (NEPS Survey Paper No. 38). Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study.

97. Vilenius-Tuohimaa, P. M., Aunola, K., & Nurmi, J. (2008). The association between mathematical word problems and reading comprehension. Educational Psychology, 28(4), 409–426. https://doi.org/10.1080/01443410701708228.

    Article  Google Scholar

98. Weinert, S., Artelt, C., Prenzel, M., Senkbeil, M., Ehmke, T., & Carstensen, C. H. (2011). Development of competencies across the life span. Zeitschrift für Erziehungswissenschaft, 14(Suppl. 2), 67–86. https://doi.org/10.1007/s11618-011-0182-7.

    Article  Google Scholar

99. Wilkinson, G. S. (1993). WRAT3 Wide Range Achievement Test: Administration manual. Wilmington: Wide Range.

    Google Scholar

100. Wohlkinger, F., Ditton, H., von Maurice, J., Haugwitz, M., & Blossfeld, H.-P. (2011). Motivational concepts and personality aspects across the life course. Zeitschrift für Erziehungswissenschaft, 14(Suppl. 2), 155–168. https://doi.org/10.1007/s11618-011-0184-5.

     Article  Google Scholar

101. Wohlkinger, F., Bayer, M., & Ditton, H. (2016). Measuring self-concept in the NEPS. In H.-P. Blossfeld, J. von Maurice, M. Bayer, & J. Skopek (Eds.), Methodological issues of longitudinal surveys (pp. 181–193). https://doi.org/10.1007/978-3-658-11994-2_11.

     Chapter  Google Scholar

102. Zinn, S., Würbach, A., Steinhauer, H. W., & Hammon, A. (2018). Attrition and selectivity of the NEPS starting cohorts: an overview of the past 8 years (NEPS Survey Paper No. 34). Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study.

Download references

Acknowledgements

Open access funding provided by University of Basel.

Author information

Affiliations

1. Department of Psychology, Division of Developmental and Personality Psychology, Switzerland, University of Basel, Missionsstrasse 62, CH-4055, Basel, Switzerland

   Mathias Holenstein & Alexander Grob

2. Institute of Secondary Education, Mathematics Education and its Disciplines, University of Education, University of Applied Sciences and Arts Northwestern Switzerland, Bahnhofstrasse 6, CH-5210, Windisch, Switzerland

   Georg Bruckmaier

Corresponding author

Correspondence to Mathias Holenstein.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Current themes of research

Holenstein's research focuses on (1) mathematical literacy and mathematical self-efficacy in school-age children and (2) on the development of academic self-concept. Bruckmaier's research focuses on (1) didactic competencies of teachers and (2) on mathematical modeling. Grob's research focuses on (1) intelligence and developmental diagnostics across childhood, adolescence, and adulthood, and (2) on early interventions to improve the life-course and academic achievement of regularly developing and disadvantaged children.

Most relevant publications in the field of Psychology of Education

Bünger, A., Urfer-Maurer, N., & Grob, A. (accepted). Multimethod assessment of attention, executive functions, and motor skills in children with and without ADHD: children's performance and parents' perceptions. Journal of Attention Disorders. doi.org/10.1177/1087054718824985

Kahl, T., Grob, A., Segerer, R., & Möhring, W. (accepted). Executive functions and visual-spatial skills predict mathematical achievement–asymmetrical associations across age. Psychological Research.

Gygi, J.T., Ledermann, T., Grob, A., Rudaz, M., & Hagmann-von Arx, P. (in press). The Reynolds Intellectual Assessment Scales (RIAS): measurement invariance across four language groups. Journal of Psychoeducational Assessment, 37, 590-602. DOI:10.1177/0734282918780565

published (sorted by year from recent to older )

Bruckmaier, G., Binder, K., Krauss, S. & Kufner, H.-M. (2019). An eye-tracking study of statistical reasoning with tree diagrams and 2 x 2 tables. Frontiers in psychology, 10(632). doi: 10.3389/fpsyg.2019.00632

Bruckmaier, G. (2019). Didaktische Kompetenzen von Mathematiklehrkräften–Weiterführende Analysen aus der COACTIV-Studie (Perspektiven der Mathematikdidaktik). Wiesbaden: Springer Spektrum. doi: 10.1007/978-3-658-26820-6

Bruckmaier, G., Binder, K. & Krauss, S. (2019). Strategien beim Lösen statistischer Aufgaben–Eine Eyetracking-Studie zur visuellen Durchmusterung von Baumdiagrammen und Vierfeldertafeln. In Fakultät für Mathematik der Universität Regensburg (Eds.), Beiträge zum Mathematikunterricht 2019. Münster: WTM.

Binder, K. & Bruckmaier, G. (2019). Geheimnisvolle Zahlentafeln. In C. Löh, S. Krauss & N. Kilbertus (Eds.), Quod erat knobelandum. Themen, Aufgaben und Lösungen des Schülerzirkels Mathematik der Universität Regensburg (pp. 189-194). Berlin: Springer Spektrum.

Binder, K. & Bruckmaier, G. (2019). Lösungsvorschläge zu Thema 17. In C. Löh, S. Krauss & N. Kilbertus (Eds.), Quod erat knobelandum. Themen, Aufgaben und Lösungen des Schülerzirkels Mathematik der Universität Regensburg (pp. 299-304). Berlin: Springer Spektrum.

Holenstein, M. & Grob, A. (2019). Mathematical literacy: an integrative view. Results from an integrative longitudinal study. In A. Grob (Chair). Results from ongoing SEED-studies. Symposium conducted at 41st International School Psychology Association Conference, Basel, Switzerland.

Manicolo, O., Brotzmann, M., Hagmann-von Arx, P., Grob, A., & Weber, P. (2019). Gait in children with infantile/atypical autism: age-dependent decrease in gait variability and associations with motor skills. European Journal of Pediatric Neurology, 23, 117-125. DOI: 10.1016/j.ejpn.2018.09.011

Wagner, L., Holenstein, M., Wepf., H., & Ruch, W. (2019). Character strengths Achievement, and Flow experiences in different learning situations. Paper presented at the 6th Swiss Conference on Positive Psychology, Bern, Switzerland.

Binder, K., Krauss, S., Bruckmaier, G. & Marienhagen, J. (2018). Visualizing the Bayesian 2-test case: the effect of tree diagrams on medical decision making. PLoS ONE, 13(3).

Bruckmaier, G., Krauss, S., & Blum, W. (2018). Aspekte des Modellierens in der COACTIV-Studie. In W. Blum & R. Borromeo Ferri (Eds.), Lehrerkompetenzen zum Mathematischen Modellieren (Mathematisches Modellieren in Schule und Hochschule) (pp. 21-55). Wiesbaden: Springer Spektrum.

Hilbert, S., Bruckmaier, G., Binder, K., Krauss, S. & Bühner, M. (2018). Prediction of elementary mathematics grades by cognitive abilities. European Journal of Psychology of Education, 33(4), 1-19.

Grob, A., & Hagmann-von Arx, P. (2018). Intelligence and Development Scales—2. Intelligenz- und Entwicklungsskalen für Kinder und Jugendliche. Hogrefe: Bern.

Hagmann-von Arx, P., Lemola, S., & Grob, A. (2018). Does IQ = IQ? Comparability of intelligence test scores in typically developing children. Assessment, 25, 691-701. DOI: 10.1177/1073191116662911

Holenstein M. & Grob A. (2018). Mathematical literacy and academic achievement: a longitudinal analysis of predictors and outcomes of mathematical competence. Poster presented at the 23th Federal Congress of School Psychology (Bundeskongress für Schulpsychologie), Frankfurt am Main, Deutschland.

Möhring, W., Klupp, S., & Grob, A. (2018). Effects of dual tasking and methylphenidate on gait in children with attention deficit hyperactivity disorder. Human Movement Science, 62, 48-57. https://doi.org/10.1016/j.humov.2018.09.007

Urfer-Maurer, N., Ludyga, S., Stalder, T., Brand, S., Holsboer-Trachsler, E., Gerber, M., Grob, A., Weber, P., & Lemola, S. (2018). Heart rate variability and salivary cortisol in very preterm children during school age. Psychoneuroendocrinology, 87, 27-34. doi: 10.1016/j.psyneuen.2017.10.004

Bruckmaier, G., Blum, W., Krauss, S. & Schmeisser, C. (2017). Aspekte professioneller Kompetenz: Ein empirischer Vergleich verschiedener Stichproben. In Institut für Mathematik der Universität Potsdam (Eds.), Beiträge zum Mathematikunterricht 2017 (pp. 131-134). Münster: WTM.

Binder, K., Krauss, S., Bruckmaier, G. & Marienhagen, J. (2017). Was bedeuten medizinische Testergebnisse wirklich? Baumdiagramme zur Visualisierung Bayesianischer Aufgaben. In Institut für Mathematik der Universität Potsdam (Eds.), Beiträge zum Mathematikunterricht 2017 (pp. 99-102). Münster: WTM.

Gygi, J.T., Hagmann-von Arx, P., Schweizer, F., & Grob, A. (2017). The predictive validity of four intelligence tests for school grades: a small sample longitudinal study. Frontiers in Psychology, 8:375. DOI: 10.3389/fpsyg.2017.00375.

Keller, K., Troesch, L.M., Loher, S., & Grob, A. (2016). Effortful control and language competence–the small but mighty difference between first and second language. Frontiers in Psychology, 7:1015. doi: 10.3389/fpsyg.2016.01015

Kölbl, M. & Bruckmaier, G. (2017). Eyetracking und Statistik – Eine Studie zu Blickbewegungen bei Diagrammen. In Institut für Mathematik der Universität Potsdam (Eds.), Beiträge zum Mathematikunterricht 2017 (pp. 1395-1396). Münster: WTM.

Binder, K., Krauss, S. & Bruckmaier, G. (2016). Visualisierung komplexer Bayesianischer Aufgaben. In Institut für Mathematik und Informatik Heidelberg (Eds.), Beiträge zum Mathematikunterricht 2016 (pp. 1469-1472). Münster: WTM.

Bruckmaier, G., Krauss, S., Blum, W. & Leiss, D. (2016). Measuring mathematics teachers' professional competence by using video clips (COACTIV video). ZDM - The International Journal on Mathematics Education, 48(1-2). doi: 10.1007/s11858-016-0772-1

Bruckmaier, G., Binder, K. & Krauss, S. (2016). Numerische Darstellungsarten statistischer Informationen. In E.-M. Plackner & N. von Schroeders (Eds.), Daten und Zufall. MaMut – Materialien für den Mathematikunterricht, 3 (pp. 47-76). Hildesheim: Franzbecker.

Manicolo, O., Grob, A., Lemola, S., & Hagmann-von Arx, P. (2016). Age related decline of gait variability in children with attention-deficit/hyperactivity disorder: support for the maturational delay hypothesis in gait. Gait and Posture, 44, 245-249. DOI: 10.1016/j.gaitpost.2015.12.012.

Binder, K., Krauss, S. & Bruckmaier, G. (2015). Effects of visualizing statistical information–an empirical study on tree diagrams and 2 x 2 tables. Frontiers in Psychology, 6(1186).

Binder, K., Krauss, S. & Bruckmaier, G. (2015). Welche Visualisierung unterstützt Bayesianisches Denken? In F. Caluori, H. Linneweber-Lammerskitten & C. Streit (Eds.), Beiträge zum Mathematikunterricht 2015 (pp. 160-163). Münster: WTM.

Bruckmaier, G, Krauss, S. & Neubrand, M. (2015). Erkennen des didaktischen Potentials zur Modellierung. In G. Kaiser & H.-W. Henn (Eds.), Werner Blum und seine Beiträge zum Modellieren im Mathematikunterricht (pp. 77-88). Wiesbaden: Springer.

Krauss, S., Bruckmaier, G., Schmeisser, C. & Brunner, M. (2015). Quantitative Forschungsmethoden in der Mathematikdidaktik. In R. Bruder, L. Hefendehl-Hebecker, B. Schmidt-Thieme & H.-G. Weigand (Eds.), Handbuch Mathematikdidaktik (pp. 611-639). Heidelberg: Springer.

Frischknecht, M.-C., Reimann, G., & Grob, A. (2015). Do parents notice deficits in child development at preschool age? Accuracy of parent estimation concerning child development. Kindheit und Entwicklung, 24, 70–77. DOI: 10.1026/0942-5403/a000162

Keller, K.L., Troesch, L.M., & Grob, A. (2015). First-born siblings show better second language skills than later born siblings. Frontiers in Psychology, 6:705. doi:10.3389/fpsyg.2015.00705

Bruckmaier, G. & Krauss, S. (2014). Prädiktive Validität von Lehrermerkmalen in der COACTIV-Studie. In J. Roth & J. Ames (Eds.), Beiträge zum Mathematikunterricht 2014 (pp. 257-260). Münster: WTM.

Krauss, S. & Bruckmaier, G. (2014). Das Experten-Paradigma in der Forschung zum Lehrerberuf. In E. Terhart, H. Bennewitz & M. Rothland (Eds.), Handbuch der Forschung zum Lehrerberuf (2^nd Ed.) (pp. 241-261). Münster: Waxmann.

Krauss, S. & Bruckmaier, G. (2014). Eignet sich die Formel von Bayes für Gerichtsverfahren? In U. Sproesser, S. Wessolowski & C. Wörn (Eds.), Daten, Zufall und der Rest der Welt (pp. 123–132). Wiesbaden: Springer.

Hagmann-von Arx, P., Perkinson-Gloor, N., Brand, S., Albert, D., Holsboer-Trachsler, E., Grob, A., Weber, P., & Lemola, S. (2014). In school-age children who were born very preterm sleep efficiency is associated with cognitive function. Neuropsychobiology, 70, 244-252. DOI: 10.1159/000369026.

Schmeisser, C., Krauss, S., Bruckmaier, G., Ufer, S. & Blum, W. (2013). Transmissive and constructivist beliefs of in-service mathematics teachers and of beginning university students. In Y. Li & J. N. Moschkovich (Eds.), Proficiency and beliefs in learning and teaching mathematics. Learning from Alan Schoenfeld and Günter Törner. Mathematics teaching and learning, 3 (pp. 51–68).Rotterdam: Sense.

Bruckmaier, G., Krauss, S., Leiss, D., Blum, W., Neubrand, M. & Brunner, M. (2013). COACTIV-Video: Eine unterrichtsnahe Erfassung fachdidaktischen Wissens mittels Videovignetten . In G. Greefrath, F. Käpnick & M. Stein (Eds.), Beiträge zum Mathematikunterricht 2013 (pp. 212–215). Münster: WTM.

Gut, J., Reimann, G., & Grob, A. (2013). A contextualized view on long-term predictors of academic performance. Journal of Educational Psychology, 105, 436-443. DOI: 10.1037/a0031503

Keller, K., Troesch, L. M., & Grob, A. (2013). Shyness as a risk factor for local language skills of immigrant preschoolers. Journal of Applied Developmental Psychology, 34, 328-335. DOI: 10.1016/j.appdev.2013.07.001

Reimann, G., Gut, J., Frischknecht, M.-C., & Grob, A. (2013). Memory abilities in children with mathematical difficulties: comorbid language difficulties matter. Learning and Individual Differences, 23, 108-113. DOI: 10.1016/j.lindif.2012.10.017

Reimann, G., Stoecklin, M., Lavallee, K., Gut, J., Frischknecht, M.-C., & Grob, A. (2013). Cognitive and motivational profile shape predicts mathematical skills over and above profile level. Psychology in the Schools, 50, 37-56. DOI: 10.1002/pits.21659

Gut, J., Reimann, G., & Grob, A. (2012). Cognitive, language, mathematical, and socioemotional skills as predictors of subsequent school performance: is a child's performance on the Intelligence Development Scales predictive of its school performance three years later? Zeitschrift für Pädagogische Psychologie, 26, 213-220. DOI: 10.1024/1010-0652/a000070

Bruckmaier, G., Krauss, S., Blum, W. & Neubrand, M. (2012). Zur Auswahl und Anordnung von Mathematik-Aufgaben – Eine Untersuchung im Rahmen der COACTIV-Studie. In M. Ludwig & M. Kleine (Eds.), Beiträge zum Mathematikunterricht 2012 (pp. 153–156). Münster: WTM.

Gut, J., Heckmann, C., Meyer, C.S., Schmid, M., & Grob, A. (2012). Language skills, mathematical thinking, and achievement motivation in children with ADHD, disruptive behavior disorders, and normal controls. Learning and Individual Differences, 22, 375-379. DOI: 10.1016/j.lindif.2011.12.002.

Bruckmaier, G., Krauss, S. & Brunner, M. (2011). Linda, Ziegen und Krankenhäuser - Neues aus dem PROLOG-Projekt. In R. Haug & L. Holzäpfel (Eds.), Beiträge zum Mathematikunterricht 2011 (pp. 167–170). Münster: WTM.

Krauss, S., Bruckmaier, G. & Martignon, L. (2010). Teaching grown-ups how to use Bayesian networks. In C. Reading (Ed.), Data and context in statistics education: towards an evidence-based society. Proceedings of the Eighth International Conference on Teaching Statistics (ICOTS8). Voorburg: International Statistical Institute.

Bruckmaier, G., Krauss, S. & Brunner, M. (2010). PROLOG: Eine Studie zum probabilistischen und logischen Denken von Jugendlichen in Luxemburg. In A. M. Lindmeier & S. Ufer (Eds.), Beiträge zum Mathematikunterricht 2010 (pp. 205–208). Münster: WTM.

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This paper uses data from the National Educational Panel Study (NEPS): Starting Cohort Grade 5, doi:https://doi.org/10.5157/NEPS:SC3:7.0.1. From 2008 to 2013, NEPS data were collected as part of the Framework Program for the Promotion of Empirical Educational Research funded by the German Federal Ministry of Education and Research (Bundesministerium für Bildung und Forschung, BMBF). Since 2014, NEPS has been carried out by the Leibniz Institute for Educational Trajectories (Leibniz-Institut für Bildungsverläufe e.V., LIfBi) at the University of Bamberg in cooperation with a nationwide network.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and Permissions

About this article

Cite this article

Holenstein, M., Bruckmaier, G. & Grob, A. Transfer effects of mathematical literacy: an integrative longitudinal study. Eur J Psychol Educ 36, 799–825 (2021). https://doi.org/10.1007/s10212-020-00491-4

Download citation

• Received: 20 January 2020

• Revised: 08 July 2020

• Accepted: 09 July 2020

• Published: 07 August 2020

• Issue Date: September 2021

• DOI : https://doi.org/10.1007/s10212-020-00491-4

Keywords

• Mathematical literacy
• Academic achievement
• Mathematical self-concept
• Secondary school
• Transfer effects

Math Lit A Pathway To College Mathematics Pdf

Source: https://link.springer.com/article/10.1007/s10212-020-00491-4

Posted by: knottgrecond.blogspot.com

Share this post